本页面将简要介绍希尔排序。
希尔排序(英语:Shell sort),也称为缩小增量排序法,是 插入排序 的一种改进版本。希尔排序以它的发明者希尔(英语:Donald Shell)命名。
排序对不相邻的记录进行比较和移动:
将待排序序列分为若干子序列(每个子序列的元素在原始数组中间距相同); 对这些子序列进行插入排序; 减小每个子序列中元素之间的间距,重复上述过程直至间距减少为 1 1 1 希尔排序实质上是一种分组插入方法。它的基本思想是: 对于n个待排序的数列,取一个小于n的整数gap(gap 被称为步长)将待排序元素分成若干个组子序列,所有距离为 gap 的倍数的记录放在同一个组中;然后,对各组内的元素进行直接插入排序。 这一趟排序完成之后,每一个组的元素都是有序的。然后减小 gap 的值,并重复执行上述的分组和排序。重复这样的操作,当 gap = 1 时,整个数列就是有序的。
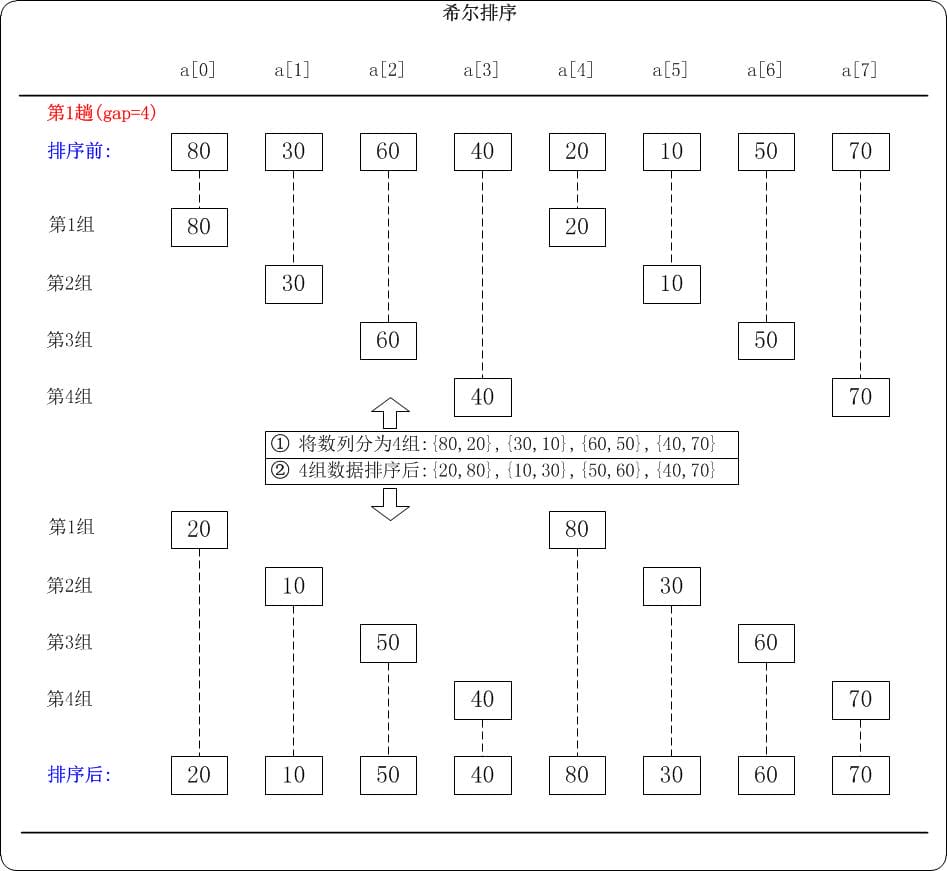
下面以数列{80, 30, 60, 40, 20, 10, 50, 70}为例,演示它的希尔排序过程。
当gap=4时,意味着将数列分为4个组: {80, 20}, {30, 10}, {60, 50}, {40, 70}。 对应数列: {80, 30, 60, 40, 20, 10, 50, 70}。{20, 80}, {10, 30}, {50, 60}, {40, 70}。{20, 10, 50, 40, 80, 30, 60, 70}
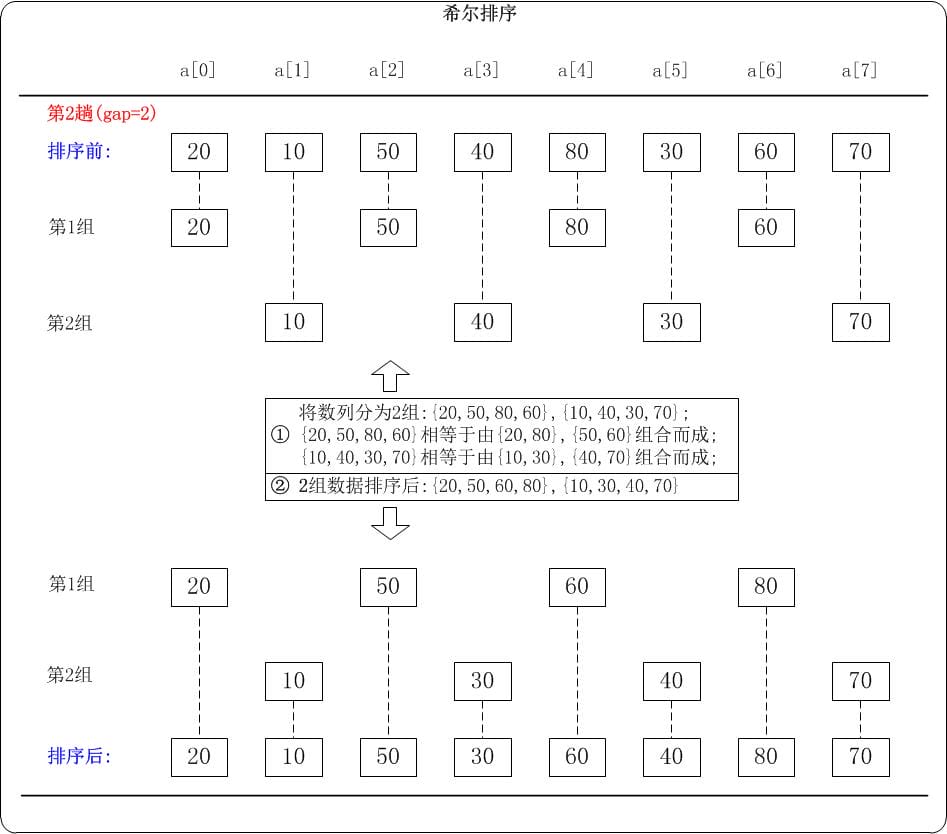
当gap=2时, 意味着将数列分为2个组: {20, 50, 80, 60}, {10, 40, 30, 70}。 对应数列: {20, 10, 50, 40, 80, 30, 60, 70} 注意: {20, 50, 80, 60}实际上有两个有序的数列{20, 80}和{50, 60}组成。 {10, 40, 30, 70}实际上有两个有序的数列{10, 30}和{40, 70}组成。{20, 50, 60, 80}, {10, 30, 40, 70}。{20, 10, 50, 30, 60, 40, 80, 70}
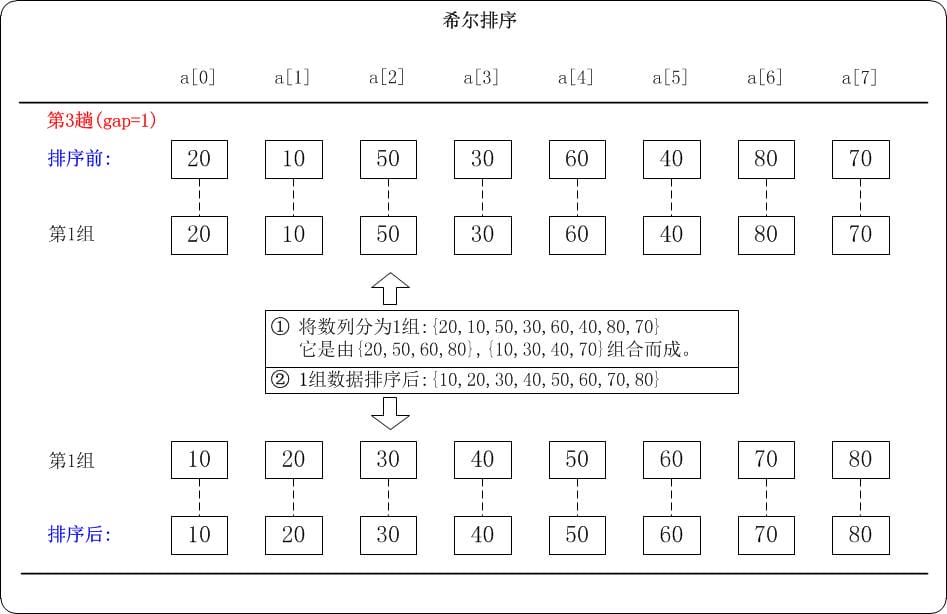
当gap=1时, 意味着将数列分为1个组: {20, 10, 50, 30, 60, 40, 80, 70} 注意: {20, 10, 50, 30, 60, 40, 80, 70}实际上有两个有序的数列{20, 50, 60, 80}和{10, 30, 40, 70}组成。{10, 20, 30, 40, 50, 60, 70, 80}
希尔排序是一种不稳定的排序算法。
希尔排序的最优时间复杂度为 O ( n ) O(n) O ( n )
希尔排序的平均时间复杂度和最坏时间复杂度与间距序列的选取有关。设间距序列为 H H H H H H o ( n 2 ) o(n^2) o ( n 2 )
命题 1 1 1 :若间距序列为 H = { 2 k − 1 ∣ k = 1 , 2 , … , ⌊ log 2 n ⌋ } H= \{ 2^k-1\mid k=1,2,\ldots,\lfloor\log_2 n\rfloor \} H = { 2 k − 1 ∣ k = 1 , 2 , … , ⌊ log 2 n ⌋} O ( n 3 / 2 ) O(n^{3/2}) O ( n 3/2 )
命题 2 2 2 :若间距序列为 H = { k = 2 p ⋅ 3 q ∣ p , q ∈ N , k ≤ n } H= \{ k=2^p\cdot 3^q\mid p,q\in \mathbb N,k\le n \} H = { k = 2 p ⋅ 3 q ∣ p , q ∈ N , k ≤ n } O ( n log 2 n ) O(n\log^2 n) O ( n log 2 n )
为证明这两个命题,我们先给出一个重要的定理并证明它,这个定理反应了希尔排序的最主要特征。
定理 1 1 1 :只要程序执行了一次 InsertionSort ( h ) \text{InsertionSort}(h) InsertionSort ( h ) InsertionSort \text{InsertionSort} InsertionSort A A A
A 1 , A 1 + h , A 1 + 2 h , … A 2 , A 2 + h , A 2 + 2 h , … ⋮ A h , A h + h , A h + 2 h , … \begin{array}{c} A_1,A_{1+h},A_{1+2h},\ldots \\ A_2,A_{2+h},A_{2+2h},\ldots \\ \vdots \\ A_h,A_{h+h},A_{h+2h},\ldots \end{array} A 1 , A 1 + h , A 1 + 2 h , … A 2 , A 2 + h , A 2 + 2 h , … ⋮ A h , A h + h , A h + 2 h , …
证明 :
我们先证明一个引理:
引理 1 1 1 :对于整数 n , m n,m n , m l l l X ( x 1 , x 2 , … , x n + l ) , Y ( y 1 , y 2 , … , y m + l ) X(x_1,x_2,\ldots,x_{n+l}),Y(y_1,y_2,\ldots,y_{m+l}) X ( x 1 , x 2 , … , x n + l ) , Y ( y 1 , y 2 , … , y m + l )
y 1 ≤ x n + 1 , y 2 ≤ x n + 2 , … , y l ≤ x n + l y_1 \le x_{n+1},y_2 \le x_{n+2},\ldots,y_l \le x_{n+l} y 1 ≤ x n + 1 , y 2 ≤ x n + 2 , … , y l ≤ x n + l
则我们将两个数组分别升序排序后,上述要求依然成立。
证明 :
设数组 X X X X ′ ( x 1 ′ , … , x n + l ′ ) X'(x'_1,\ldots,x'_{n+l}) X ′ ( x 1 ′ , … , x n + l ′ ) Y Y Y Y ′ ( y 1 ′ , … , y m + l ′ ) Y'(y'_1,\ldots,y'_{m+l}) Y ′ ( y 1 ′ , … , y m + l ′ )
对于任何 1 ≤ i ≤ l 1\le i\le l 1 ≤ i ≤ l x n + i ′ x'_{n+i} x n + i ′ X ′ X' X ′ l − i l-i l − i X X X l − i l-i l − i X X X X ′ X' X ′
那么在可重集合 { x n + 1 , … , x n + l } ⊂ X \{x_{n+1},\ldots,x_{n+l} \} \subset X { x n + 1 , … , x n + l } ⊂ X x n + i ′ x'_{n+i} x n + i ′ l − i l-i l − i
进而小于 x n + i ′ x'_{n+i} x n + i ′ i i i i i i x n + k 1 , x n + k 2 , … , x n + k i x_{n+k_1},x_{n+k_2},\ldots,x_{n+k_i} x n + k 1 , x n + k 2 , … , x n + k i
y k 1 ≤ x n + k 1 ≤ x n + i ′ , y k 2 ≤ x n + k 2 ≤ x n + i ′ , … , y k i ≤ x n + k i ≤ x n + i ′ y_{k_1}\le x_{n+k_1}\le x'_{n+i},y_{k_2}\le x_{n+k_2}\le x'_{n+i},\ldots,y_{k_i}\le x_{n+k_i}\le x'_{n+i} y k 1 ≤ x n + k 1 ≤ x n + i ′ , y k 2 ≤ x n + k 2 ≤ x n + i ′ , … , y k i ≤ x n + k i ≤ x n + i ′
所以 x n + i ′ x'_{n+i} x n + i ′ Y Y Y Y ′ Y' Y ′ i i i y i ′ ≤ x n + i ′ ( 1 ≤ i ≤ l ) y'_i\le x'_{n+i}\,(1\le i\le l) y i ′ ≤ x n + i ′ ( 1 ≤ i ≤ l )
证毕
再回到原命题的证明:
我们实际上只需要证明调用完 InsertionSort ( h ) \text{InsertionSort}(h) InsertionSort ( h ) InsertionSort ( k ) \text{InsertionSort}(k) InsertionSort ( k ) h h h
执行完 InsertionSort ( h ) \text{InsertionSort}(h) InsertionSort ( h )
A 1 , A 1 + h , A 1 + 2 h , … A 2 , A 2 + h , A 2 + 2 h , … ⋮ A h , A h + h , A h + 2 h , … \begin{array}{c} A_1,A_{1+h},A_{1+2h},\ldots \\ A_2,A_{2+h},A_{2+2h},\ldots \\ \vdots \\ A_h,A_{h+h},A_{h+2h},\ldots \end{array} A 1 , A 1 + h , A 1 + 2 h , … A 2 , A 2 + h , A 2 + 2 h , … ⋮ A h , A h + h , A h + 2 h , …
而之后执行 InsertionSort ( k ) \text{InsertionSort}(k) InsertionSort ( k )
A 1 , A 1 + k , A 1 + 2 k , … A 2 , A 2 + k , A 2 + 2 k , … ⋮ A k , A k + k , A k + 2 k , … \begin{array}{c} A_1,A_{1+k},A_{1+2k},\ldots \\ A_2,A_{2+k},A_{2+2k}, \ldots \\ \vdots \\ A_k,A_{k+k},A_{k+2k},\ldots \end{array} A 1 , A 1 + k , A 1 + 2 k , … A 2 , A 2 + k , A 2 + 2 k , … ⋮ A k , A k + k , A k + 2 k , …
对于每个 i i i ( 1 ≤ i ≤ min ( h , k ) ) (1\le i\le \min(h,k)) ( 1 ≤ i ≤ min ( h , k ))
A i , A i + k , A i + 2 k , … … , A i + h , A i + h + k , A i + h + 2 k , … \begin{array}{c} A_i,A_{i+k},A_{i+2k},\ldots \\ \ldots,A_{i+h},A_{i+h+k},A_{i+h+2k},\ldots \end{array} A i , A i + k , A i + 2 k , … … , A i + h , A i + h + k , A i + h + 2 k , …
第二个组前面也加上“… \ldots … i + h ≥ k i+h\ge k i + h ≥ k
则第二个组就是引理 1 1 1 X X X Y Y Y l l l i + h i+h i + h n n n … \ldots … m m m l l l
又因为有:
A i ≤ A i + h , A i + k ≤ A i + h + k , … A_i\le A_{i+h},A_{i+k}\le A_{i+h+k},\ldots A i ≤ A i + h , A i + k ≤ A i + h + k , …
所以由引理 1 1 1 InsertionSort ( k ) \text{InsertionSort}(k) InsertionSort ( k ) A i ≤ A i + h ( 1 ≤ i ≤ min ( h , k ) ) A_i\le A_{i+h}\,(1\le i\le \min(h,k)) A i ≤ A i + h ( 1 ≤ i ≤ min ( h , k ))
若有 i > min ( h , k ) i>\min(h,k) i > min ( h , k ) w w w ( 1 ≤ w ≤ min ( h , k ) ) (1\le w\le \min(h,k)) ( 1 ≤ w ≤ min ( h , k )) k k k i i i
综合以上论述便有:执行完 InsertionSort ( k ) \text{InsertionSort}(k) InsertionSort ( k ) A i ≤ A i + h ( 1 ≤ i ≤ n − h ) A_i\le A_{i+h}\,(1\le i\le n-h) A i ≤ A i + h ( 1 ≤ i ≤ n − h )
得证。
证毕
这个定理揭示了希尔排序在特定集合 H H H h h h i i i
接下来我们单拎出来一个数论引理进行证明。这个定理在 OI 界因 小凯的疑惑 一题而大为出名。而在希尔排序复杂度的证明中,它也使得定理 1 1 1
引理 2 2 2 :若 a , b a,b a , b { a x + b y ∣ x , y ∈ N } \{ax+by\mid x,y\in \mathbb N \} { a x + b y ∣ x , y ∈ N } a b − a − b ab-a-b ab − a − b
证明 :
分两步证明:
先证明方程 a x + b y = a b − a − b ax+by=ab-a-b a x + b y = ab − a − b x , y x,y x , y
若无非负整数的限制,容易得到两组解 ( b − 1 , − 1 ) , ( − 1 , a − 1 ) (b-1,-1),(-1,a-1) ( b − 1 , − 1 ) , ( − 1 , a − 1 )
通过其通解形式 x = x 0 + t b , y = y 0 − t a x=x_0+tb,y=y_0-ta x = x 0 + t b , y = y 0 − t a b − 1 − b = − 1 b-1-b=-1 b − 1 − b = − 1
当 t t t x x x y y y
故不可能有非负整数解。
再证明对任意整数 c > a b − a − b c > ab-a-b c > ab − a − b a x + b y = c ax+by=c a x + b y = c
我们找一组解 ( x 0 , y 0 ) (x_0,y_0) ( x 0 , y 0 ) 0 ≤ x 0 < b 0\le x_0 < b 0 ≤ x 0 < b
则有:
b y 0 = c − a x 0 ≥ c − a ( b − 1 ) > a b − a − b − a b + a = − b by_0=c-ax_0\ge c-a(b-1)>ab-a-b-ab+a=-b b y 0 = c − a x 0 ≥ c − a ( b − 1 ) > ab − a − b − ab + a = − b
所以 b ( y 0 + 1 ) > 0 b(y_0+1) > 0 b ( y 0 + 1 ) > 0 b > 0 b>0 b > 0 y 0 + 1 > 0 y_0+1>0 y 0 + 1 > 0 y 0 ≥ 0 y_0\ge 0 y 0 ≥ 0
所以 ( x 0 , y 0 ) (x_0,y_0) ( x 0 , y 0 )
综上得证。
证毕
而下面这个定理则揭示了引理 2 2 2 1 1 1
定理 2 2 2 :如果 gcd ( h t + 1 , h t ) = 1 \gcd(h_{t+1},h_t)=1 g cd( h t + 1 , h t ) = 1 InsertionSort ( h t + 1 ) \text{InsertionSort}(h_{t+1}) InsertionSort ( h t + 1 ) InsertionSort ( h t ) \text{InsertionSort}(h_t) InsertionSort ( h t ) InsertionSort ( h t − 1 ) \text{InsertionSort}(h_{t-1}) InsertionSort ( h t − 1 ) O ( n h t + 1 h t h t − 1 ) O\left(\dfrac{nh_{t+1}h_t}{h_{t-1}} \right) O ( h t − 1 n h t + 1 h t ) j j j i i i O ( h t + 1 h t h t − 1 ) O\left(\dfrac{h_{t+1}h_t}{h_{t-1}} \right) O ( h t − 1 h t + 1 h t )
证明 :
对于 j ≤ h t + 1 h t j\le h_{t+1}h_t j ≤ h t + 1 h t i i i O ( h t + 1 h t h t − 1 ) O\left(\dfrac{h_{t+1}h_t}{h_{t-1}} \right) O ( h t − 1 h t + 1 h t )
故以下假设 j > h t + 1 h t j>h_{t+1}h_t j > h t + 1 h t
对于任意的正整数 k k k 1 ≤ k ≤ j − h t + 1 h t 1\le k\le j-h_{t+1}h_t 1 ≤ k ≤ j − h t + 1 h t h t + 1 h t − h t + 1 − h t < h t + 1 h t ≤ j − k ≤ j − 1 h_{t+1}h_t-h_{t+1}-h_t<h_{t+1}h_t\le j-k\le j-1 h t + 1 h t − h t + 1 − h t < h t + 1 h t ≤ j − k ≤ j − 1
又因为 gcd ( h t + 1 , h t ) = 1 \gcd(h_{t+1},h_t)=1 g cd( h t + 1 , h t ) = 1 2 2 2 a , b a,b a , b a h t + 1 + b h t = j − k ah_{t+1}+bh_t=j-k a h t + 1 + b h t = j − k
即得:
k = j − a h t + 1 − b h t k=j-ah_{t+1}-bh_t k = j − a h t + 1 − b h t
由定理 1 1 1
A j − b h t ≤ A j − ( b − 1 ) h t ≤ … ≤ A j − h t ≤ A j A_{j-bh_t}\le A_{j-(b-1)h_t}\le \ldots\le A_{j-h_t}\le A_j A j − b h t ≤ A j − ( b − 1 ) h t ≤ … ≤ A j − h t ≤ A j
与
A j − b h t − a h t + 1 ≤ A j − b h t − ( a − 1 ) h t + 1 ≤ … ≤ A j − b h t − h t + 1 ≤ A j − b h t A_{j-bh_t-ah_{t+1}}\le A_{j-bh_t-(a-1)h_{t+1}}\le \ldots\le A_{j-bh_t-h_{t+1}}\le A_{j-bh_t} A j − b h t − a h t + 1 ≤ A j − b h t − ( a − 1 ) h t + 1 ≤ … ≤ A j − b h t − h t + 1 ≤ A j − b h t
综合以上既有:A k = A j − a h t + 1 − b h t ≤ A j A_k=A_{j-ah_{t+1}-bh_t}\le A_j A k = A j − a h t + 1 − b h t ≤ A j
所以对于任何 1 ≤ k ≤ j − h t + 1 h t 1\le k\le j-h_{t+1}h_t 1 ≤ k ≤ j − h t + 1 h t A k ≤ A j A_k\le A_j A k ≤ A j
在 Shell-Sort 伪代码中 i i i h t − 1 h_{t-1} h t − 1 O ( h t + 1 h t h t − 1 ) O\left(\dfrac{h_{t+1}h_t}{h_{t-1}} \right) O ( h t − 1 h t + 1 h t ) i ≤ j − h t + 1 h t i\le j-h_{t+1}h_t i ≤ j − h t + 1 h t A i ≤ A j A_i\le A_j A i ≤ A j
证明完对于每个 j j j
∑ j = h t − 1 + 1 n O ( h t + 1 h t h t − 1 ) = O ( n h t + 1 h t h t − 1 ) \sum_{j=h_{t-1}+1}^n{O\left(\frac{h_{t+1}h_t}{h_{t-1}} \right)}=O\left(\frac{nh_{t+1}h_t}{h_{t-1}}\right) j = h t − 1 + 1 ∑ n O ( h t − 1 h t + 1 h t ) = O ( h t − 1 n h t + 1 h t )
得证。
证毕
认真观察定理 2 2 2 A A A h h h k k k h h h k k k 2 2 2
有了这两个定理,我们可以命题 1 1 1 2 2 2
先证明命题 1 1 1
证明 :
将 H H H
H ( h 1 = 1 , h 2 = 3 , h 3 = 7 , … , h ⌊ log 2 n ⌋ = 2 ⌊ log 2 n ⌋ − 1 ) H(h_1=1,h_2=3,h_3=7,\ldots,h_{\lfloor \log_2 n\rfloor}=2^{\lfloor \log_2 n\rfloor}-1) H ( h 1 = 1 , h 2 = 3 , h 3 = 7 , … , h ⌊ l o g 2 n ⌋ = 2 ⌊ l o g 2 n ⌋ − 1 )
Shell-Sort 执行顺序为:InsertionSort ( h ⌊ log 2 n ⌋ ) , InsertionSort ( h ⌊ log 2 n ⌋ − 1 ) , … , InsertionSort ( h 2 ) , InsertionSort ( h 1 ) \text{InsertionSort}(h_{\lfloor \log_2 n\rfloor}),\text{InsertionSort}(h_{\lfloor \log_2 n\rfloor-1}),\ldots,\text{InsertionSort}(h_2),\text{InsertionSort}(h_1) InsertionSort ( h ⌊ l o g 2 n ⌋ ) , InsertionSort ( h ⌊ l o g 2 n ⌋ − 1 ) , … , InsertionSort ( h 2 ) , InsertionSort ( h 1 )
分两部分去分析复杂度:
对于前面的若干个满足 h t ≥ n h_t\ge \sqrt{n} h t ≥ n h t h_t h t InsertionSort ( h t ) \text{InsertionSort}(h_t) InsertionSort ( h t ) O ( n 2 h t ) O\left(\dfrac{n^2}{h_t} \right) O ( h t n 2 )
考虑对最接近 n \sqrt{n} n h k h_k h k
O ( n 2 h t ) = O ( n 3 / 2 ) O\left(\frac{n^2}{h_t} \right)=O(n^{3/2}) O ( h t n 2 ) = O ( n 3/2 )
而对于 i > k i> k i > k h i h_i h i 2 h i < h i + 1 2h_i< h_{i+1} 2 h i < h i + 1
O ( n 2 h i ) = O ( n 3 / 2 / 2 i − k ) ( i > k ) O\left(\frac{n^2}{h_i} \right)=O(n^{3/2}/2^{i-k})\,(i>k) O ( h i n 2 ) = O ( n 3/2 / 2 i − k ) ( i > k )
所以大等于 n \sqrt n n
∑ i = k ⌊ log 2 n ⌋ O ( n 3 / 2 / 2 i − k ) = O ( n 3 / 2 ) \sum_{i=k}^{\lfloor \log_2 n\rfloor}{O(n^{3/2}/2^{i-k})}=O(n^{3/2}) i = k ∑ ⌊ l o g 2 n ⌋ O ( n 3/2 / 2 i − k ) = O ( n 3/2 )
对于后面剩下的满足 h t < n h_t< \sqrt{n} h t < n O ( n 3 / 2 ) O(n^{3/2}) O ( n 3/2 ) h t h_t h t 2 2 2
O ( n h t + 2 h t + 1 h t ) = O ( n h t + 2 ⋅ h t + 2 / 2 h t + 2 / 4 ) = O ( n h t + 2 ) O\left(\frac{nh_{t+2}h_{t+1}}{h_t} \right)=O\left(\frac{nh_{t+2}\cdot h_{t+2}/2}{h_{t+2}/4} \right)=O(nh_{t+2}) O ( h t n h t + 2 h t + 1 ) = O ( h t + 2 /4 n h t + 2 ⋅ h t + 2 /2 ) = O ( n h t + 2 )
再次利用 2 h i < h i + 1 2h_i < h_{i+1} 2 h i < h i + 1 k k k
2 O ( n 3 / 2 ) + ∑ i = 1 k − 3 O ( n h i + 1 ) = O ( n 3 / 2 ) + ∑ i = 1 k − 3 O ( n h k − 1 / 2 k − i − 3 ) = O ( n 3 / 2 ) + O ( n h k − 1 ) = O ( n 3 / 2 ) 2O(n^{3/2})+\sum_{i=1}^{k-3}{O(nh_{i+1})}=O(n^{3/2})+\sum_{i=1}^{k-3}{O(nh_{k-1}/2^{k-i-3})}=O(n^{3/2})+O(nh_{k-1})=O(n^{3/2}) 2 O ( n 3/2 ) + i = 1 ∑ k − 3 O ( n h i + 1 ) = O ( n 3/2 ) + i = 1 ∑ k − 3 O ( n h k − 1 / 2 k − i − 3 ) = O ( n 3/2 ) + O ( n h k − 1 ) = O ( n 3/2 )
综上可得总时间复杂度即为 O ( n 3 / 2 ) O(n^{3/2}) O ( n 3/2 )
证毕
再证明命题 2 2 2
证明 :
注意到一个事实:如果已经执行过了 InsertionSort ( 2 ) \text{InsertionSort}(2) InsertionSort ( 2 ) InsertionSort ( 3 ) \text{InsertionSort}(3) InsertionSort ( 3 ) 2 ⋅ 3 − 2 − 3 = 1 2\cdot 3-2-3=1 2 ⋅ 3 − 2 − 3 = 1 2 2 2 i i i InsertionSort ( 1 ) \text{InsertionSort}(1) InsertionSort ( 1 ) O ( n ) O(n) O ( n )
更进一步:如果已经执行过了 InsertionSort ( 4 ) \text{InsertionSort}(4) InsertionSort ( 4 ) InsertionSort ( 6 ) \text{InsertionSort}(6) InsertionSort ( 6 ) InsertionSort ( 2 ) \text{InsertionSort}(2) InsertionSort ( 2 ) InsertionSort ( 3 ) \text{InsertionSort}(3) InsertionSort ( 3 ) InsertionSort ( 2 ) \text{InsertionSort}(2) InsertionSort ( 2 ) InsertionSort ( 1 ) \text{InsertionSort}(1) InsertionSort ( 1 ) O ( n ) O(n) O ( n ) 2 2 2
不断归纳,就可以得到:如果已经执行过了 InsertionSort ( 2 h ) \text{InsertionSort}(2h) InsertionSort ( 2 h ) InsertionSort ( 3 h ) \text{InsertionSort}(3h) InsertionSort ( 3 h ) InsertionSort ( h ) \text{InsertionSort}(h) InsertionSort ( h ) O ( n ) O(n) O ( n )
接下来分为两部分分析复杂度:
对于 h t > n / 3 h_t>n/3 h t > n /3 InsertionSort ( h t ) \text{InsertionSort}(h_t) InsertionSort ( h t ) O ( n 2 / h t ) O(n^2/h_t) O ( n 2 / h t )
而 n 2 / h t < 3 n n^2/h_t<3n n 2 / h t < 3 n O ( n ) O(n) O ( n )
而这一部分元素个数是 O ( log 2 n ) O(\log^2 n) O ( log 2 n ) O ( n log 2 n ) O(n\log^2 n) O ( n log 2 n )
对于 h t ≤ n / 3 h_t\le n/3 h t ≤ n /3 3 h t ≤ n 3h_t\le n 3 h t ≤ n InsertionSort ( 2 h t ) \text{InsertionSort}(2h_t) InsertionSort ( 2 h t ) InsertionSort ( 3 h t ) \text{InsertionSort}(3h_t) InsertionSort ( 3 h t ) InsertionSort ( h t ) \text{InsertionSort}(h_t) InsertionSort ( h t ) O ( n ) O(n) O ( n )
还是一样的,这一部分元素个数也是 O ( log 2 n ) O(\log^2 n) O ( log 2 n ) O ( n log 2 n ) O(n\log^2 n) O ( n log 2 n )
综上可得总时间复杂度即为 O ( n log 2 n ) O(n\log^2 n) O ( n log 2 n )
证毕
希尔排序的空间复杂度为 O ( 1 ) O(1) O ( 1 )
代码实现
C++
Java C++ Python
Java
public class ShellSort { /** * 希尔排序 * * 参数说明: * a -- 待排序的数组 * n -- 数组的长度 */ public static void shellSort1 ( int [] a , int n ) { // gap为步长,每次减为原来的一半。 for ( int gap = n / 2 ; gap > 0 ; gap /= 2 ) { // 共gap个组,对每一组都执行直接插入排序 for ( int i = 0 ;i < gap; i ++ ) { for ( int j = i + gap; j < n; j += gap) { // 如果a[j] < a[j-gap],则寻找a[j]位置,并将后面数据的位置都后移。 if (a[j] < a[j - gap]) { int tmp = a[j]; int k = j - gap; while (k >= 0 && a[k] > tmp) { a[k + gap] = a[k]; k -= gap; } a[k + gap] = tmp; } } } } } /** * 对希尔排序中的单个组进行排序 * * 参数说明: * a -- 待排序的数组 * n -- 数组总的长度 * i -- 组的起始位置 * gap -- 组的步长 * * 组是"从i开始,将相隔gap长度的数都取出"所组成的! */ public static void groupSort ( int [] a , int n , int i , int gap ) { for ( int j = i + gap; j < n; j += gap) { // 如果a[j] < a[j-gap],则寻找a[j]位置,并将后面数据的位置都后移。 if (a[j] < a[j - gap]) { int tmp = a[j]; int k = j - gap; while (k >= 0 && a[k] > tmp) { a[k + gap] = a[k]; k -= gap; } a[k + gap] = tmp; } } } /** * 希尔排序 * * 参数说明: * a -- 待排序的数组 * n -- 数组的长度 */ public static void shellSort2 ( int [] a , int n ) { // gap为步长,每次减为原来的一半。 for ( int gap = n / 2 ; gap > 0 ; gap /= 2 ) { // 共gap个组,对每一组都执行直接插入排序 for ( int i = 0 ;i < gap; i ++ ) groupSort (a, n, i, gap); } } public static void main ( String [] args ) { int i ; int a [] = { 80 , 30 , 60 , 40 , 20 , 10 , 50 , 70 }; System . out . printf ( "before sort:" ); for (i = 0 ; i < a . length ; i ++ ) System . out . printf ( "%d " , a[i]); System . out . printf ( " \n " ); shellSort1 (a, a . length ); //shellSort2(a, a.length); System . out . printf ( "after sort:" ); for (i = 0 ; i < a . length ; i ++ ) System . out . printf ( "%d " , a[i]); System . out . printf ( " \n " ); } } C++
template < typename T > void shell_sort ( T array [], int length ) { int h = 1 ; while (h < length / 3 ) { h = 3 * h + 1 ; } while (h >= 1 ) { for ( int i = h; i < length; i ++ ) { for ( int j = i; j >= h && array [j] < array [j - h]; j -= h) { std :: swap ( array [j], array [j - h]); } } h = h / 3 ; } } Python
def shell_sort ( array , length ): h = 1 while h < length / 3 : h = int ( 3 * h + 1 ) while h >= 1 : for i in range (h, length): j = i while j >= h and array[j] < array[j - h]: array[j], array[j - h] = array[j - h], array[j] j -= h h = int (h / 3 ) 排序 - Shell排序(Shell Sort)